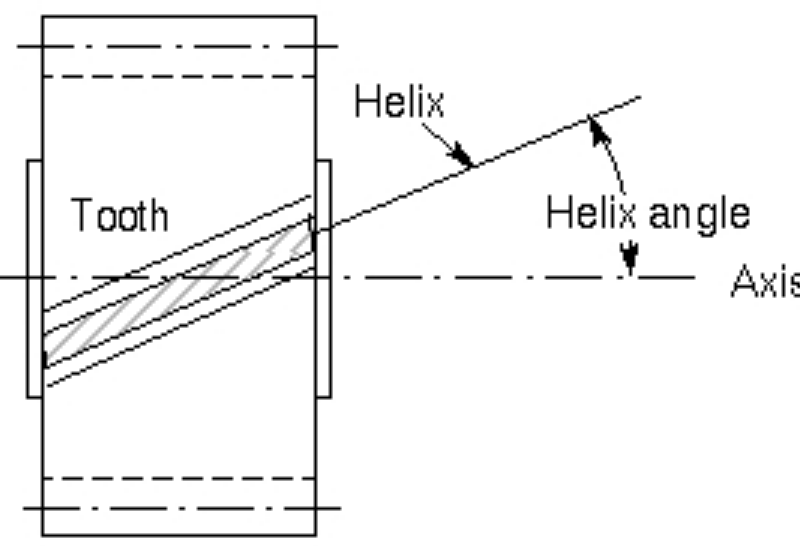
The helix angle (“the HA” or “θ” ), a fundamental geometric concept, plays a pivotal role in diverse engineering disciplines and natural occurrences. Its influence can be observed in structures as varied as screws and turbine blades to DNA and spiral galaxies. Understanding the helix angle allows for a deeper comprehension of these diverse applications and unravels the elegance of this captivating spiral geometry.
Definition and Geometric Representation of Helix Angle
The HA is a fundamental geometric property that describes the angle formed between the axis of the spiral and a reference plane, typically perpendicular to the axis. This angle is a defining characteristic of spiral structures and holds significant importance in various engineering applications and natural phenomena.
Geometric Representation
To envision a spiral and grasp its geometric form, one must imagine a thread or wire wound around a cylinder or cone in a continuous spiral manner. As the thread wraps around the central axis, it forms a spiral structure. The HA (θ) represents the angle formed between the tangent to any point on the spiral’s cross-section and the reference plane perpendicular to the axis:
- The HA can be understood as the “tilt” or “inclination” of the spiral concerning the base plane. It determines the steepness or fineness of the spiral and affects its overall shape and behavior;
- For instance, let’s consider an everyday screw. The threaded part of the screw forms a spiral structure. In this case, the HA is the angle between the screw’s axis (an imaginary line passing through its center) and the plane perpendicular to the axis. This angle influences the screw’s advancement during rotation and its ability to effectively fasten and unfasten materials.
In nature, one of the most well-known examples of a spiral structure is the double helix of DNA. The HA in DNA refers to the angle between the axis of the DNA molecule and a plane perpendicular to it. This angle is crucial for understanding the structure of DNA and how it carries and encodes genetic information.

The Connection between Helix Angle, Pitch, and Diameter
The pitch of a spiral is the distance traveled along the axis in one complete turn of the spiral. It is a critical parameter that, along with the diameter of the spiral, influences the HA. Increasing the pitch reduces the HA, resulting in a tighter and steeper spiral. Conversely, reducing the pitch increases the HA, creating a wider and shallower spiral.
| Parameter | Definition | Relationship to HA (θ) |
|---|---|---|
| Helix Angle (θ) | The angle between the helix axis and a plane perpendicular to the axis. | – As the pitch increases, the HA tends to decrease, resulting in a tighter and steeper spiral. – As the pitch decreases, the HAtends to increase, creating a broader and shallower spiral. – The HA is directly related to the radius (diameter) and pitch of the helix. |
| Pitch | The distance traveled along the axis for one complete turn of the helix. | – Increasing the pitch will lead to a smaller HA. – Decreasing the pitch will result in a larger HA. |
| Diameter (Radius) | The distance from the center of the helix to a point on the helix’s cross-section. | – The HA is inversely proportional to the diameter. Smaller diameter leads to larger HA, and vice versa. |
It is essential to note that the relationship between these parameters can vary depending on whether the spiral is right-handed (clockwise) or left-handed (counterclockwise). In the table, we assume a right-handed spiral, which is more commonly encountered in various applications. For left-handed spirals, the angle sign will be negative, but the dependencies remain the same.
Mathematical Expressions for Helix Angle
θ can be mathematically calculated using trigonometric functions and geometric relationships. For a right-handed spiral (one that moves upwards and away from the viewer in a clockwise direction when looking along the axis), the HA can be determined using the tangent function:
tan(θ) = pitch / (2π * radius)
Where:
- θ – the HA in radians;
- pitch – the distance traveled along the axis in one complete turn of the spiral;
- radius – the distance from the center of the spiral to a point on its cross-section;
- For left-handed spirals (those moving counterclockwise when looking along the axis), the same formula applies, but the angle sign will be negative.
It is important to note that θ is usually expressed in radians. If it needs to be converted to degrees, one can use the conversion factor: 1 radian ≈ 57.3 degrees. Therefore, after calculating the angle in radians, if necessary, it can be converted to degrees by multiplying it approximately by 57.3.
Helix Angle in Different Applications
θ finds diverse applications in various fields, including engineering, aerospace technology, biology, architecture, art, astrophysics, and nanotechnology. Its significance in each of these areas contributes to enhancing the efficiency, functionality, and aesthetics of structures and systems. Here are some prominent examples:
Engineering:
- Cylindrical Gears: θ in gear systems influences the smoothness and efficiency of power transmission between intersecting shafts. Helical gears are widely used in engineering and the automotive industry due to their ability to withstand high loads and minimize noise and vibration;
- Spiral Springs: θ determines the mechanical properties of spiral springs, such as stiffness and load-bearing capacity. These springs are used in various devices and systems for absorbing and storing mechanical energy.
Aerospace Technology:
- Aircraft Propellers: θ of an aircraft propeller affects the thrust generated during rotation. Optimizing θ enhances propeller efficiency, leading to improved aircraft performance and fuel economy;
- Wing Design: Some aircraft wings have a spiral shape, known as “wing twist,” which optimizes the distribution of lift along the wing span. This twist reduces drag and enhances overall aerodynamic characteristics.
Biology and Bioengineering:
- Double Helix of DNA: θ is fundamental to the structure of DNA—the genetic material that carries essential information in living organisms. The specific θ provides stability and facilitates processes like replication and transcription, which are crucial for life;
- Protein Structure: Proteins often have spiral structures, such as alpha helices and beta sheets, which are essential for their functioning and stability. Understanding the angles of protein folding is vital for studying their structure and interactions.
Architecture and Art:
- Architectural Projects: Inspired by spirals, constructions are used in buildings and structures to create visually impressive facades, staircases, and ramps. The dynamic form of spirals adds a unique aesthetic dimension to architectural masterpieces;
- Sculptures: Artists use the angles of spirals in their sculptures to convey a sense of movement and fluidity. The inherent elegance of spirals is a popular choice in contemporary art.
Astrophysics:
- Spiral Galaxies: Spiral galaxies, such as our Milky Way, exhibit characteristic spiral structures. θ in these galaxies plays a role in their rotational dynamics and provides valuable insights into the formation and evolution of galaxies;
- Interstellar Phenomena: Spiral-like structures, such as jets emanating from black holes and rotating stars, are encountered in various interstellar phenomena. Understanding θ helps decipher these cosmic phenomena.
The versatility and significance of θ in various scientific and technical fields are remarkable. From optimizing mechanical systems and improving aircraft performance to understanding the fundamental structures of DNA and proteins, θ plays a crucial role in shaping our world and expanding our knowledge of the universe.
As technology advances and research progresses, harnessing the potential of the helix angle promises even more innovative solutions and discoveries in the future.
Importance of Helix Angle Optimization
The optimization of θ holds great importance for diverse engineering and scientific applications. Precise tuning and maximizing θ enable designers and researchers to achieve specific goals, enhance efficiency, and improve the functionality of a wide range of systems. Here are several key reasons why θ optimization is significant:
- Improvement of Mechanical Characteristics: In engineering, optimizing θ in components such as helical gears and springs can lead to improved mechanical characteristics. By selecting an appropriate θ, engineers can increase load-bearing capacity, reduce friction, and minimize wear, resulting in enhanced equipment efficiency and reliability;
- Enhancement of Propulsion Efficiency: In aerospace technology, optimizing θ in aircraft propellers and wings can significantly impact propulsion efficiency. A carefully chosen θ in propeller design can lead to increased thrust, reduced energy consumption, and improved flight performance;
- Stability and Functionality of Biomolecules: In biology and bioengineering, understanding and optimizing θ in biomolecules such as DNA and proteins are crucial. A specific θ in the double helix structure of DNA ensures stability, accurate replication, and transcription during cell division and genetic information transfer. In proteins, θ determines their secondary and tertiary structures, directly influencing their functions;
- Aesthetic Appeal and Structural Integrity: In architecture and art, designs inspired by the spiral can provide both aesthetic appeal and structural integrity. Optimizing θ in architectural constructions and sculptures allows for visually appealing forms while ensuring stability and load distribution within the structure;
- Understanding Astrophysical Phenomena: In astrophysics, studying θ of celestial structures, such as spiral galaxies and interstellar jets, provides valuable insights into their formation, evolution, and dynamic behavior. Understanding θ helps researchers unravel the mysteries of the universe on a grand scale;
- Nanoscale Precision and Functionality: In nanotechnology, optimizing θ in nanoscale structures and devices enables precise control of their properties and functionalities. Nanomaterials with specific helix angles can be created for targeted drug delivery, electronics, and other cutting-edge applications;
- Energy Efficiency and Performance Boost: In various applications, from mechanical systems to aerospace propulsion, optimizing θ can lead to increased energy efficiency and performance. Minimizing unnecessary friction, resistance, and energy losses through the optimal HA can result in cost savings and enhanced system performance;
- Biomimetic Design and Innovations: In nature, spiral-like structures are frequently used, and by optimizing the HA in designs, researchers can obtain biomimetic solutions that mimic the efficiency and elegance of nature. Such an approach opens possibilities for creating innovative technologies and solutions inspired by natural examples.
Optimizing the HA plays a crucial role in unlocking the full potential of various engineering designs and natural phenomena. Whether in mechanical systems, aerospace technology, biology, art, or nanotechnology, fine-tuning the HA can lead to increased productivity, stability, functionality, and efficiency.
By understanding and harnessing the power of this geometric property, scientists, engineers, and designers can continue pushing the boundaries of innovation and enhancing our surrounding world.
Conclusions
The fundamentals of the helix angle encompass its definition, geometric representation, and mathematical relationships between the angle, pitch, and diameter. As a critical parameter in various engineering and natural systems, optimizing the HA is pivotal in achieving desired outcomes across different fields of application.
A deeper understanding of this geometric concept paves the way for innovative developments and advancements in diverse domains, from mechanical engineering to nanotechnology.